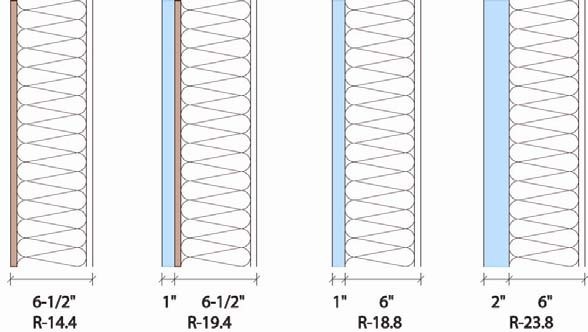
Additional Thermal Resistance
With rising utility cost, designing homes to be more energy efficient is increasing in importance. Part of the overall efficiency of a house is the thermal resistance of the various enclosure assemblies. Common residential construction use wall framing based on either 2x4 or 2x6 dimensional lumber with insulation installed in the stud cavities created by the framing members. With cavity insulation the overall thermal resistance can be varied somewhat, by using different types of insulation, varying the installation methods, and varying the stud spacing, but there is still a limit because of the depth of the stud cavity.
Adding insulating sheathing to the exterior of the assembly is a simple method of increasing the overall thermal resistance of the wall assembly beyond that possible with cavity insulations and thereby increasing the overall efficiency of the house.
When examining the overall thermal resistance of the wall assembly, the effective R-value must be considered. A simple method than can be used to estimate the effective R-value of the cavity space is through using the isothermal planes method set out in Chapter 25 of the ASHRAE Fundamentals 2005. While this method is not as accurate as some other more sophisticated computer simulation models, it is a means to get a rough idea of the effective insulating value of an assembly. With the isothermal method, the effective R-value of the cavity assembly is a proportional sum of the various U-values of the different components based on material fractions.
U(cavity) = U(studs)·F(studs) + U(insulation)·F(insulation)
Where:
U(cavity) = average U value of the insulation and studs U(studs) = U value of wood framing
U(insulation) = U value of cavity insulation
F(studs) = fraction of area of studs, headers, and sill plates
F(insulation) = fraction of area of insulation
Therefore the effective R-value of the cavity can be expressed as:
R(cavity) = 1/U(cavity)
The overall R-value of the assembly is a sum of the thermal resistance of all of the components.
Where:
R(total) = R(comp 1) + R(comp 2) + … + R(comp n)
R(total) = total R-value of the assembly
R(comp) = individual effective R-value of each material layer
As an example the effective cavity insulation value and the total effective R-value for various assemblies were calculated. The fiberglass batt or blown cellulose may be rated as R-19, however due to the wood studs and other framing members the effective thermal resistance may be as much as 35% less than the rated cavity insulation, leaving an effective value of only R-12.5 for the cavity as seen in the calculations below.
The effective R-value of the following assembly with a 23% framing fraction is:
R(cavity)= 1/[(0.77/19)+(0.23/5.83)]
R(cavity)= 12.5
R(total) = 0.17+0.62+12.5+0.45+0.68
R(total)= 14.42
Insulating sheathing provides additional insulation to the house that is run continuous past the exterior face of the wood studs. Because of this the rated R-value for the insulating sheathing is very close to the effective R-value of the insulating sheathing in the assembly. With the lack of framing penetrating through the layer insulating sheathing, the whole R-value can be generally be used. This allows for large increases in the effective R-value of the assembly without substantially increasing the thickness of the wall.
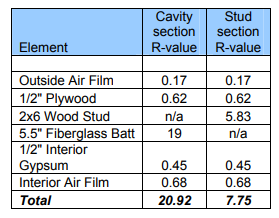
Incorporating 1 inch of rigid insulation into the design of the previous example wall assembly yields the following effective R-value for the assembly:
R(cavity)= 1/[(0.77/19)+(0.23/5.83)]
R(cavity)= 12.5
R(total)= 0.17+5+0.62+12.5+0.45+0.68
R(total)= 19.42
Adding one inch of insulating sheathing (R-5 for this example) will increase a 2x6 stud wall from an effective R-14.4 to an effective R-19.4. This represents an increase of 35% effective thermal resistance with only 15% increase in the overall wall thickness.
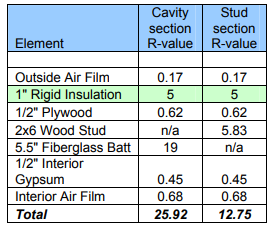
If the insulating sheathing is used as the primary sheathing (eliminating the plywood or OSB from the exterior)
R(cavity)= 1/[(0.77/19)+(0.23/5.83)]
R(cavity)= 12.5
R(total)= 0.17+5+12.5+0.45+0.68
R(total)= 18.80
With this configuration the wall thickness is only increased by 8% while the effective thermal resistance increases from R-14.4 to R-18.8, a 31% increase.
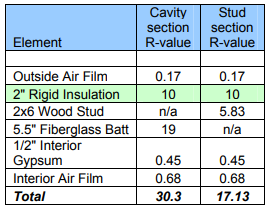
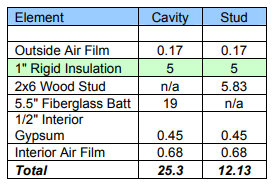
Incorporating 2 inches of rigid insulation into the design of the example wall assembly yields the following effective R-value for the assembly:
R(cavity)= 1/[(0.77/19)+(0.23/5.83)]
R(cavity)= 12.5
R(total)= 0.17+10+12.5+0.45+0.68
R(total)= 23.80
Adding two inches of rigid insulation to the exterior (R-10) will increase the effective R-value from R-14.4 to R-23.8. This represents an increase of 65% over the original effective R-value.